# 毒药和老鼠
题目:1000 瓶毒药里面只有 1 瓶是有毒的,毒发时间为 1 个星期,问需要多少只老鼠才能在 1 个星期后试出那瓶有毒。
# 解题思路
分组法
- 简单说就是通过将 1000 个瓶子分成比如 100 组,每组 10 个瓶子,让老鼠分别去喝这 100 组,有可能第一只老鼠就中毒死了,也有可能最后一只老鼠才死,所以第一轮最好情况是一次找到,最坏是 100 次找到,平均需要 50 次找到,波动太大。且第一轮只找到哪 10 个瓶子中有毒药,所以还需要再用老鼠来测。。。所以这种方式是不合理的。
二分法
- 二分法的思路就是将 1000 瓶每次均分为一半,用一只老鼠去喝其中一半的混合水,就能验出哪部分有毒药。依次法,在进行 9 次二分(也就是用了 9 只老鼠)后,还剩最终 2 瓶药水,用最后一只老鼠去喝其中一瓶,一定会得到最终是哪瓶有毒。即 10 只老鼠可以得到结论,因为 2 的 10 次方为 1024,可以刚好 cover 住 1000 瓶。
- 但这种方法是不符合题意的。。毒发时间是 1 个星期后,而给定时间也刚好是 1 个星期后就要出结果。。二分法却需要每次二分后都等 1 个星期,也就是 10 个星期后才能出结果。
二进制法(译码器法)
- 正解,下面是详细解读
# 二进制法实现
1000 个瓶子太多了,我们简化下题目,来讲解思路。
3 位二进制可以表示 8 个数,那么我们就假定有 8 个瓶子(编号 0~7),使用 3 只老鼠(ABC)去测。
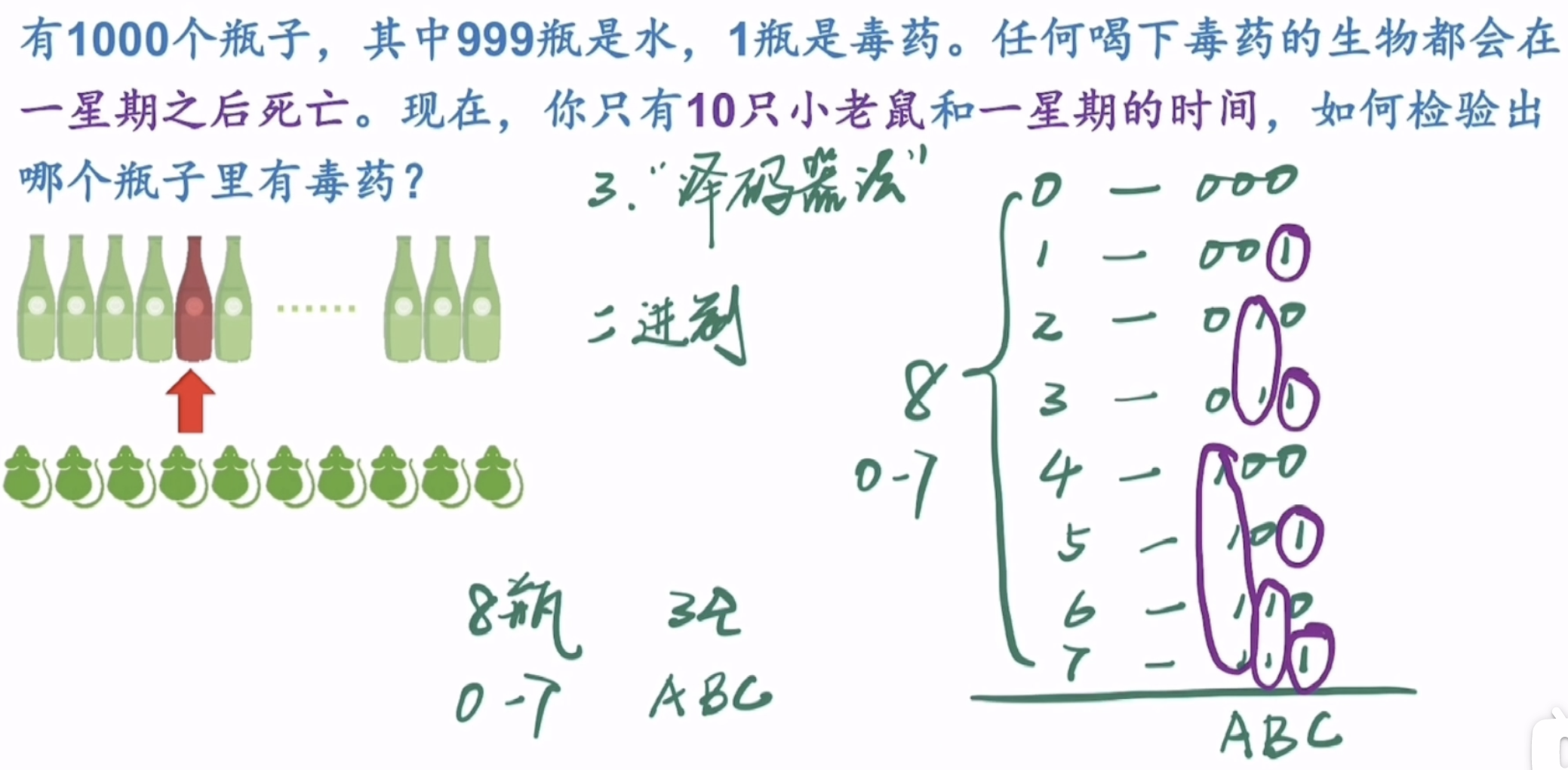
我们让每只老鼠都只喝对应位数上为 1 的瓶子水,即 ABC 三只老鼠分别喝:
A: 4 5 6 7
B: 2 3 6 7
C: 1 3 5 7
那么 1 个星期后,某个老鼠死掉了,就说明对应的那一位中数字为 1 的瓶子是毒药,而没死的老鼠对应的位数,数字为 0 的瓶子是毒药。
这样做交叉判断后就能得出唯一的毒药是哪瓶。
比如 AC 死掉了,B 活着,则说明瓶子编号为 101,即编号为 5 的瓶子是毒药。而且是同时进行验证的,一星期后就能得出结论。
那么回到我们的题目,依次法,3 位二进制编号 8 个数,那么 1000 个瓶子,需要 1024 个数,也就是 2 的 10 次方,10 位二进制来编号(0~999 号),则可以验出。
# 扩展题:两个星期和最少老鼠
扩展题:如果你有两个星期的时间(换句话说你可以做两轮实验),为了从 1000 个瓶子中找出毒药,你最少需要几只老鼠?注意,在第一轮实验中死掉的老鼠,就无法继续参与第二次实验了。
三进制:逢三进一,退一还三,用 0、1、2 三个数字表示,从个位往左分别是个位、3 位、9 位,27 位...以此类推。 比如 11 的三进制表示是 102
答:7 只老鼠就足够了。事实上,7 只老鼠足以从 3^7 = 2187 个瓶子中找出毒药来(而 3^6 = 729 不够 cover1000 瓶)。
首先,把所有瓶子从 0 到 999 编号,然后全部转换为 7 位三进制数。现在,让第一只老鼠喝掉所有三进制数右起第一位是 2 的瓶子,让第二只老鼠喝掉所有三进制数右起第二位是 2 的瓶子,等等。一星期之后,如果第一只老鼠死了,就知道毒药瓶子的三进制编号中,右起第一位是 2;如果第二只老鼠没死,就知道毒药瓶子的三进制编号中,右起第二位不是 2,只可能是 0 或者 1……也就是说,每只死掉的老鼠都用自己的生命确定出了,三进制编号中自己负责的那一位是 2;但每只活着的老鼠都只能确定,它所负责的那一位不是 2。于是,问题就归约到了只剩一个星期时的情况。在第二轮实验里,让每只活着的老鼠继续自己未完成的任务,喝掉它负责的那一位是 1 的所有瓶子。再过一星期,毒药瓶子的三进制编号便能全部揭晓了。
总结:n 只小白鼠和 t 周的时间可以从(t+1)^n 个瓶子中检验出毒药(一瓶)来。
