# 链表中环的入口结点
leetcode - 142. 环形链表 II (opens new window)
# 1、题目描述
给定一个链表,返回链表开始入环的第一个节点。如果链表无环,则返回 null。
为了表示给定链表中的环,我们使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始)。 如果 pos 是 -1,则在该链表中没有环。
说明:不允许修改给定的链表。
示例 1:
输入:head = [3,2,0,-4], pos = 1
输出:tail connects to node index 1
解释:链表中有一个环,其尾部连接到第二个节点。
# 2、思路
第一步:确定一个链表是否有环。这一步就是
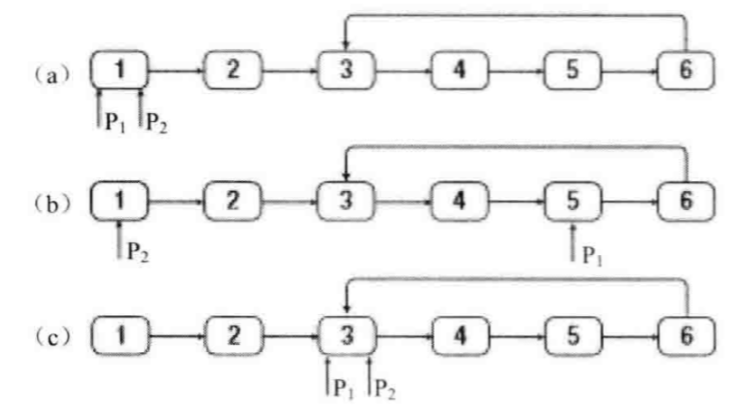
快慢指针法,定义两个指针,同时从链表的头结点出发,快指针一次走两步,慢指针一次走一步。如若有环,两个指针必定相遇,也就是如果快指针反追上了慢指针,说明存在环(这里要注意,两指针相遇的地方一定在环中,但不一定是环的入口),如果快指针走到了链表的末尾(指向了NULL),则说明不存在环。第二步:找到环的入口点。这还是可以
利用双指针来解决,两个指针初始都指向头结点,如果我们可以知道环中的结点个数,假设为n,那么第一个指针先向前走n步,然后两个指针(另一个从头结点开始)同时向前,当两个指针再次相遇时,他们的相遇点正好就是环的入口点。
# Johninch
# 快慢指针法
- 时间复杂度O(n)
- 空间复杂度O(1)
// 环形链表的入口节点
// 方法:分两步
// 阶段一 快慢指针判断是否成环,相遇必定成环,快指针走到链尾指向null则无环;
// 阶段二 如果成环,记录第一次相遇的节点firstMeet,使用两个慢指针(即步频为1的)一个从head,一个从firstMeet出发,相遇时从head出发的指针则为入环点
function detectCycle(head) {
// 阶段1:快慢指针,速度fast步频2,slow步频1,试图找出第一次相遇的点,判断是否成环
let fast = head, slow = head, firstMeet = null
while(slow && fast && fast.next) {
slow = slow.next
fast = fast.next.next
if(slow === fast) {
// 相遇时,慢指针走的路程就是 相遇点firstMeet
firstMeet = slow
break
}
}
if(!firstMeet) {
// 没有相遇,不成环
return null
}
// 阶段2:用 阶段1中找到的 相遇点firstMeet 来找到环的入口
// 设定head到入环点为n,假设环路大于n,环内路被分为b与n。
// 慢指针从入环处开始跑b步,距离入环处就剩下了n。
// 此时,快指针则是从距离入环处n步远的位置开始跑了2b步,距离入环处也是剩下了n。
// 慢指针在圈内b的位置,快指针在圈内n+2b(减去圈长n+b也是b的位置),位置相同
// 所以他们相遇了,距离入环处都是n,这个点就是firstMeet
// 所以最后,使用两个slow指针,一个从head出发,一个从firstMeet出发,都走n步,相遇,返回从head出发的slow即可
// 另外,对于环路小于n的情况,则可将多个小环展开视为一个大环,情况是一样的
while(firstMeet && head) {
if(firstMeet === head) {
return head
}
firstMeet = firstMeet.next
head = head.next
}
return null
}
# 会不会跨过去
会不会跨过去?
注意到:我们在快慢指针的方法中,设定快慢指针的速度分别为2和1,如果成环,那么二者为什么一定会相遇而不是刚好快指针跨过慢指针呢?
这样思考:二者相差速度为1,如果把慢跑者视作参考系,则意味着慢跑者站着不动,快跑者的速度为1,而最小间隔是1,因此一定会相遇。
如果速度是其他值呢,比如是2和4呢?
二者相差是2,最小距离为1,所以真的是有可能跨过去的!
# 使用Set缓存
- 时间复杂度O(n)
- 空间复杂度O(n)
判断链表是否成环,设置一个缓存,将每个链表节点都存起来,如果重复出现,就是有环的,否则就没有环:
function detectCycle(head) {
const cache = new Set()
while(head) {
if (cache.has(head)) {
return true
} else {
cache.add(head)
}
head = head.next
}
return false
}
