链表练习题集合：1、从尾到头打印链表；2、删除链表中重复的结点；3、合并两个有序链表；4、反转链表；5、链表中倒数第k个结点；6、两个链表的第一个公共结点；7、链表中环的入口结点；8、复杂链表的复制；

构建基础链表及功能：

class Node {
  constructor(value, next) {
    this.value = value
    this.next = next
  }
}

class List {
  constructor() {
    this.head = new Node(null, null)
  }

  find(index) {
    let current = this.head
    for (let i = 0; i < index; ++i) {
      current = current.next
    }

    return current;
  }

  insert(value, index) {
    const prev = this.find(index)
    const next = new Node(value, prev.next)
    prev.next = next
  }
}

从尾到头打印链表

1、题目描述

输入一个链表，按链表值从尾到头的顺序返回一个ArrayList。

2、思路

(三种方法：借助栈、递归、列表的首位插入)

从头到尾打印链表比较简单，从尾到头很自然的可以想到先将链表进行反转，然后再打印。但是，通常我们不希望改变原链表的结构，这是一个只读操作。

进一步分析，这是一个典型的“后入先出”的思想，因此很自然的可以想到用栈来实现，每遍历一个结点，可以将其压入栈中，遍历结束后再逐个弹栈，将结点值存入ArrayList，这样就实现了从尾到头的打印。

更进一步，既然想到了用栈，那一定可以通过递归来实现。每访问到一个结点，先递归输出其后的结点，再输出该结点自身即可。

另外，当我们使用Java或者python语言时，有一种比较巧妙的方法就是使用列表的插入方法，每次插入数据，都总是插入到首位，这样得到的List就是从尾到头的链表序列。

3、代码实现

let list = new List()
list.insert('a', 0)
list.insert('b', 1)
list.insert('c', 2)
list.insert('d', 3)
list.insert('e', 4)

console.log(list)

// 递归法：
function printFromTailToHead(node) {
  node.next && printFromTailToHead(node.next)
  node.value && console.log(node.value)
}

let result = printFromTailToHead(list.head)

console.log(result)

删除链表中重复的结点

1、题目描述

删除有序链表中重复的结点，重复的结点不保留，返回链表头指针。 例如，链表1->2->3->3->4->4->5 处理后为 1->2->5。

2、思路

删除重复结点，也就是如果当前结点和下一个结点的值相同，那么就是重复的结点，都可以被删除，为了保证删除之后的链表的连通性，在删除之后，要把当前结点前面的结点和下一个没有重复的结点链接起来，为此，程序需要记录当前的最后一个不重复结点，即程序中的pre。重点在于：一定要确保当前链接到链表中的一定是不会再重复的结点，具体见代码实现。

关于第一个结点如果重复怎么办的问题，我们不用单独考虑，可以使用链表中一贯的做法，加一个头结点即可。

3、代码实现

// 注意这里的前提是 有序链表、不保留重复节点
function deleteDuplication(pHead) {
  if (pHead === null || pHead.next === null) { // 只有0个或1个节点，则返回
    return pHead;
  }

  var dummy = new Node(null, null);
  dummy.next = pHead; // 创建一个虚拟节点，让其位于头节点之前，以处理第一个节点重复的问题

  var pre = dummy;
  var cur = pHead;

  while (cur !== null && cur.next !== null) {
    if (cur.next.val === cur.val) { // 当前节点是重复节点
      var curRepetitiveVal = cur.val;
      while (cur !== null && cur.val === curRepetitiveVal) {
        // 跳过值与当前节点相同的全部节点,找到第一个与当前节点不同的节点
        cur = cur.next;
      }
      pre.next = cur; // 跳过重复节点，前后连接
    } else { // 当前节点不重复，整体前移
      pre = cur;
      cur = cur.next;
    }
  }

  return dummy.next;
}

// 注意这里的前提是 有序链表、保留重复节点
function deleteDuplication(pHead) {
  if (pHead === null || pHead.next === null) { // 链表为空或只有 1个节点，则返回
    return pHead;
  }

  var dummy = new Node(null, null);
  dummy.next = pHead; // 创建一个虚拟节点，让其位于头节点之前，以处理第一个节点重复的问题

  var pre = dummy;
  var cur = pHead;

  while (cur !== null && cur.next !== null) {
    if (cur.next.val === cur.val) { // 当前节点是重复节点
      pre = cur // 保留重复节点，在发现重复时，pre指针立刻指向重复节点的第一个
      var curRepetitiveVal = cur.val;
      while (cur !== null && cur.val === curRepetitiveVal) {
        // 跳过值与当前节点相同的全部节点,找到第一个与当前节点不同的节点
        cur = cur.next;
      }
      pre.next = cur; // 跳过重复节点，前后连接
    } else { // 当前节点不重复，整体前移
      pre = cur;
      cur = cur.next;
    }
  }

  return dummy.next;
}

function duplicateDelete(list){
    let pre = list;
    let cur = list.next;
    let next = cur.next;
    let flag = false;// 用于标志当前节点和下一节点值是否重复

    while(next){
        if(cur.value === next.value){ // 删除重复的节点
            flag = true;
            next = next.next;
            cur.next = next;
        } else{
            if(flag){ // 不保留重复节点时，要把保留的一个重复节点删除
                cur = next;
                next = cur.next;
                pre.next = cur;
                flag = false;
            } else{
                pre = next;
                cur = next
                next = next.next;
            }
        }
    }
}

合并两个有序链表

1、题目描述

输入两个递增排序的链表，合并这两个链表并使新链表中的结点仍然是按照递增排序的。

2、思路

准备一个指针node，假设指向两个链表中节点的指针分别是：p1和p2。

比较p1和p2的value大小
如果，p1.value 小于 p2.value, node.next 指向 p1, p1 向后移动
否则，node.next 指向 p2, p2 向后移动
重复第 1 步，直到其中一个链表遍历完
跳出循环，将 node.next 指向未遍历完的链表的剩余部分
整个过程的时间复杂度是 O(N), 空间复杂度是 O(1)

3、代码实现

// 非递归
function merge(p1, p2) {
  if (!p1) {
    return p2
  } else if (!p2) {
    return p1
  }

  let head = new Node() // 增加头节点
  let node = head

  while (p1 && p2) {
    if (p1.value < p2.value) {
      node.next = p1
      p1 = p1.next
    } else {
      node.next = p2
      p2 = p2.next
    }

    node = node.next
  }

  if (p1) {
    node.next = p1
  }

  if (p2) {
    node.next = p2
  }

  return head.next;
}


// 递归
function merge(p1, p2) {
  if (!p1) {
    return p2
  } else if (!p2) {
    return p1
  }

  let head = null // 头节点
  if (p1.value < p2.value) {
    head = p1
    head.next = merge(p1.next, p2)
  } else {
    head = p2
    head.next = merge(p1, p2.next)
  }

  return head
}

反转链表

1、题目描述

输入一个链表，反转链表后，输出新链表的表头。

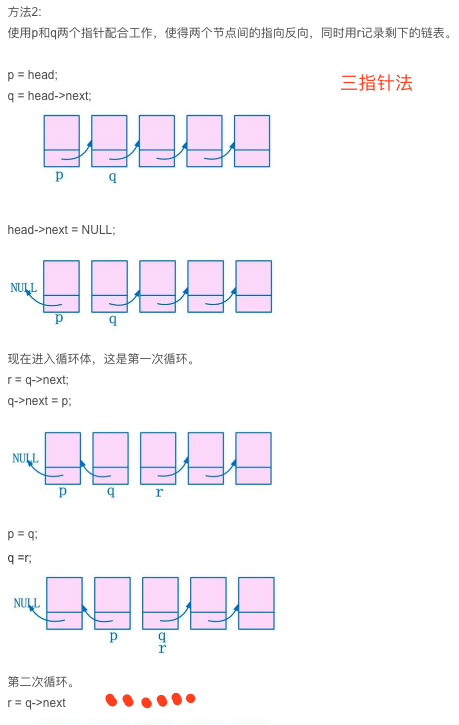
2、思路

有两种方法可以实现：（1）三指针（原地反转）。使用三个指针，分别指向当前遍历到的结点、它的前一个结点以及后一个结点。将指针反转后，三个结点依次前移即可；（2）链表头插法(注意这里是往head后插)。从第二个节点开始依次插入到第一个节点之后，最后将第一个节点挪到新表结尾；（3）递归方法。同样可以采用递归来实现反转。将头结点之后的链表反转后，再将头结点接到尾部即可。

3、代码实现

// https://blog.csdn.net/feliciafay/article/details/6841115

// ”三指针法“：使用p、q 两个节点间的指向反向，同时用 临时指针r 来记录剩下的链表
// 链表原地操作，时间复杂度是 O(N)，但是空间复杂度只有 O(1)
function reverseList(head) {
  if (head === null || head.next === null) {    // 链表为空或只有一个节点时，不用反转
    return head;
  }
  let p = head
  let q = head.next;
  head.next = null;    // 让原本的head变为尾节点

  let r;    // 临时指针
  while (q) { // 当q为null时，反转完毕
    r = q.next; // 保留下一个step要处理的指针
    q.next = p; // 这一步使p、q的指向反向

    p = q; // p、q后移
    q = r;
  }

  return p; // 此时 p 就是反转后链表的 头结点
}

// ”链表头插法“：从第2个节点到第N个节点，依次逐节点插入到第1个节点(head节点)之后，最后将第一个节点挪到新表的表尾。
// 时间复杂度是 O(N)，空间复杂度也是 O(N)
function reverseList(head) {
  if (head === null || head.next === null) {    // 链表为空或只有一个节点时，不用反转
    return head;
  }
  let p = head.next // 从第二个节点操作
  let q
  while (p.next) {
    q = p.next

    p.next = q.next
    q.next = head.next
    head.next = q
  }

  p.next = head // 成环
  head = p.next.next // 新head变为原head的next
  p.next.next = null // 断掉环

  return head
}


// ”递归“：对于树的大部分问题，基本可以考虑用递归来解决。但是我们不太熟悉的一点是，对于单链表的一些问题，也可以使用递归。
// 可以认为单链表是一颗永远只有左(右)子树的树，因此可以考虑用递归来解决:
// 现在需要把A->B->C->D进行反转，
// 可以先假设B->C->D已经反转好，已经成为了D->C->B,那么接下来要做的事情就是将D->C->B看成一个整体，让这个整体的next指向A，所以问题转化了反转B->C->D。那么，
// 可以先假设C->D已经反转好，已经成为了D->C,那么接下来要做的事情就是将D->C看成一个整体，让这个整体的next指向B，所以问题转化了反转C->D。那么，
// 可以先假设D(其实是D->NULL)已经反转好，已经成为了D(其实是head->D),那么接下来要做的事情就是将D(其实是head->D)看成一个整体，让这个整体的next指向C，所以问题转化了反转D。
// 上面这个过程就是递归的过程
function reverseList(head) {
  if (head === null || head.next === null) {
    return head;
  }
  // console.log('递归前')
  var new_head = reverseList(head.next);  // 反转后的头节点
  // var temp = new_head
  // console.log('>>>>>>>>>>>>>', JSON.stringify(temp))
  // console.log('++++++++', JSON.stringify(head.next.next), JSON.stringify(head)) // JSON.stringify(head.next.next)为null
  // console.log('递归后')

  head.next.next = head; // 将反转后的链表的尾节点与当前节点相连
  head.next = null;

  return new_head;
}

链表中倒数第k个结点

1、题目描述

输入一个链表，输出该链表中倒数第k个结点。为了符合习惯，从1开始计数，即链表的尾结点是倒数第1个节点。例如，一个链表有6个结点，从头结点开始，它们的值依次是1,2,3,4,5,6。则这个链表倒数第三个结点是值为4的结点。

2、思路

对于单链表来说，没有从后向前的指针，因此一个直观的解法是先进行一次遍历，统计出链表中结点的个数n，第二次再进行一次遍历，找到第n-k+1个结点就是我们要找的结点，但是这需要对链表进行两次遍历。

为了实现一次遍历，我们这里采用双指针解法（快慢指针）。我们可以定义两个指针，第一个指针从链表的头指针开始先向前走k步，第二个指针保持不动，从第k+1步开始，第二个指针也从头开始前进，两个指针都每次前进一步。这样，两个指针的距离都一直保持在k，当快指针（走在前面的）到达null时，慢指针（走在后面的）正好到达第k个结点。注意：要时刻留意空指针的判断。

3、代码实现

// 方法1：遍历两遍，第一遍得出链表长度n，第二遍遍历到第n-k+1个节点即为所求

// 方法2：快慢指针
function findKthFromTail(head, k) {
  if (!head || k <= 0) {
    return null;
  }

  let fast = head,
    slow = head;

  for (let i = 0; i < k; ++i) {
    fast = fast.next;
    if (!fast) {
      return null;
    }
  }

  while (fast) {
    slow = slow.next;
    fast = fast.next;
  }

  return slow;
}

/**
 * 以下是测试代码, 分别输出倒数第2、3和5个节点
 */

let node3 = new Node(3, null),
  node2 = new Node(2, node3),
  node1 = new Node(1, node2),
  head = new Node(0, node1);

console.log(findKthFromTail(head, 2));
console.log(findKthFromTail(head, 3));
console.log(findKthFromTail(head, 5));

两个链表的第一个公共结点

1、题目描述

输入两个链表，找出它们的第一个公共结点。

2、思路

方法一：借助辅助栈。我们可以把两个链表的结点依次压入到两个辅助栈中，这样两个链表的尾结点就位于两个栈的栈顶，接下来比较两个栈顶的结点是否相同。如果相同，则把栈顶弹出继续比较下一个，直到找到最后一个相同的结点。此方法也很直观，时间复杂度为O(m+n)，但使用了O(m+n)的空间，相当于用空间换取了时间效率的提升。

方法二：快慢指针（将两个链表设置成一样长）。具体做法是先求出两个链表各自的长度，然后将长的链表的头砍掉，也就是长的链表先走几步，使得剩余的长度与短链表一样长，这样同时向前遍历便可以得到公共结点。时间复杂度为O(m+n)，不需要额外空间。

3、代码实现

// 方法1：栈实现 时间为O(m+n)，空间为O(m+n)
// 在第一个公共节点前的节点都是不相同的，因此只要倒序遍历两个链表，找出最后一个出现的相同节点即可。
// 因为链表不能倒序遍历，所以借助栈实现。
function findCommon(list1, list2) {
  const stack1 = [],
    stack2 = [];

  let node = list1;
  while (node) {
    stack1.push(node);
    node = node.next;
  }

  node = list2;
  while (node) {
    stack2.push(node);
    node = node.next;
  }

  node = null;
  while (stack1.length && stack2.length) {
    let top1 = stack1.pop(),
      top2 = stack2.pop();
    if (top1 === top2) {
      node = top1;
    } else {
      break;
    }
  }

  return node;
}

// 方法2：快慢指针 时间为O(m+n)，不需要额外空间
// 假设链表 A 长度大于链表 B 长度，它们的长度差为 diff。
// 让 A 的指针先移动 diff 的位移，然后 A 和 B 的指针再同时向后移动，每次比较节点，选出第一个出现的相同节点。
function findCommon(list1, list2) {
  let length1 = 0,
    length2 = 0;

  let node = list1;
  while (node) {
    ++length1;
    node = node.next;
  }

  node = list2;
  while (node) {
    ++length2;
    node = node.next;
  }

  let diff = Math.abs(length1 - length2),
    longList = null,
    shortList = null;
  if (length1 > length2) {
    longList = list1;
    shortList = list2;
  } else {
    longList = list2;
    shortList = list1;
  }

  while (diff > 0) {
    longList = longList.next;
    --diff;
  }

  while (longList && shortList) {
    if (longList === shortList) {
      return longList;
    }
    longList = longList.next;
    shortList = shortList.next;
  }

  return null;
}

// 测试代码
const node4th = new Node(4);
const node3th = new Node(3, node4th);
const list1 = new Node(1, new Node(2, new Node(3, node3th)));
const list2 = new Node(5, new Node(6, node3th));

console.log(findCommon(list1, list2));

链表中环的入口结点

1、题目描述

给一个链表，若其中包含环，请找出该链表的环的入口结点，否则，输出null。

2、思路

第一步：确定一个链表是否有环。这一步就是快慢指针法，定义两个指针，同时从链表的头结点出发，快指针一次走两步，慢指针一次走一步。如若有环，两个指针必定相遇，也就是如果快指针反追上了慢指针，说明存在环（这里要注意，两指针相遇的地方一定在环中，但不一定是环的入口），如果快指针走到了链表的末尾（指向了NULL），则说明不存在环。

第二步：找到环的入口点。这还是可以利用双指针来解决，两个指针初始都指向头结点，如果我们可以知道环中的结点个数，假设为n，那么第一个指针先向前走n步，然后两个指针（另一个从头结点开始）同时向前，当两个指针再次相遇时，他们的相遇点正好就是环的入口点。

3、代码实现

// 环形链表的入口节点
// 方法：分两步
// 阶段一 快慢指针判断是否成环，相遇必定成环，快指针走到链尾指向null则无环；
// 阶段二 如果成环，记录第一次相遇的节点firstMeet，使用两个慢指针(即步频为1的)一个从head，一个从firstMeet出发，相遇时从head出发的指针则为入环点

function detectCycle(head) {

  // 阶段1：快慢指针，速度fast步频2，slow步频1，试图找出第一次相遇的点，判断是否成环
  let fast = head, slow = head, firstMeet = null
  while(slow && fast && fast.next) {
      slow = slow.next
      fast = fast.next.next
      if(slow === fast) {
          // 相遇时，慢指针走的路程就是 相遇点firstMeet
          firstMeet = slow
          break
      }
  }

  if(!firstMeet) {
      // 没有相遇，不成环
      return null
  }

  // 阶段2：用 阶段1中找到的 相遇点firstMeet 来找到环的入口
  // 设定head到入环点为n，假设环路大于n，环内路被分为b与n。
  // 慢指针从入环处开始跑b步，距离入环处就剩下了n。
  // 此时，快指针则是从距离入环处n步远的位置开始跑了2b步，距离入环处也是剩下了n。
  // 慢指针在圈内b的位置，快指针在圈内n+2b（减去圈长n+b也是b的位置），位置相同
  // 所以他们相遇了，距离入环处都是n，这个点就是firstMeet
  // 所以最后，使用两个slow指针，一个从head出发，一个从firstMeet出发，都走n步，相遇，返回从head出发的slow即可
  // 另外，对于环路小于n的情况，则可将多个小环展开视为一个大环，情况是一样的
  while(firstMeet && head) {
      if(firstMeet === head) {
          return head
      }
      firstMeet = firstMeet.next
      head = head.next
  }
  return null
}